Sistema numerico ottale

Il sistema numerico ottale (spesso abbreviato come ott o oct) è un sistema numerico posizionale in base 8, cioè che utilizza solo 8 simboli (tipicamente 0, 1, 2, 3, 4, 5, 6, 7) invece dei 10 del sistema numerico decimale usato comunemente.

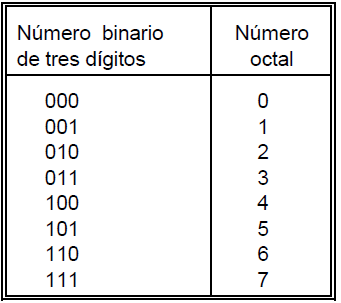
I numeri ottali (insieme ai numeri binari e esadecimali) vengono diffusamente utilizzati in svariati campi della scienza e della tecnica, in particolare nell'ambito informatico, in quanto una cifra ottale è esattamente equivalente, dal punto di vista del significato numerico, a tre cifre binarie. Generalmente, risulta scomodo trattare lunghe stringhe in bit: così si fa uso di sistemi numerici che consentano di esprimere in maniera più compatta le lunghe stringhe di 0 e 1.

Ecco una tabella che confronta le rappresentazioni binarie, ottali e decimali ed esadecimali dei numeri dallo zero al quindici:

Perciò il numero decimale settantanove, ad esempio, la cui rappresentazione binaria è ${\displaystyle 0100\ 1111}$, può essere scritto come 117 in ottale.

Definizione matematica (conversione in base 10)

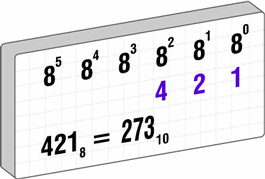
La formula per convertire un numero da ottale a decimale (dove con ${\displaystyle d_{n}}$ si indica la cifra di posizione ${\displaystyle n}$ all'interno del numero, partendo da 0) è $${\displaystyle d_{(n-1)}\;8^{(n-1)} \ldots d_{0}\;8^{0}=N}$$

Il numero ottale ${\displaystyle c_{2}c_{1}c_{0}}$ equivale al numero ${\displaystyle c_{2}\times 8^{2} c_{1}\times 8^{1} c_{0}\times 8^{0}}$. Ad esempio ${\displaystyle 543_{8}}$, dove ${\displaystyle c_{2}=5,c_{1}=4,c_{0}=3}$, equivale al numero

${\displaystyle 543_{8}=5\times 8^{2} 4\times 8^{1} 3\times 8^{0}=320 32 3=355_{10}.}$

Metodi di conversione

Da ottale in binario

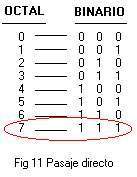
Dato un numero in base ottale ${\displaystyle (c_{1},c_{2},\ldots ,c_{n})_{8}}$ di ${\displaystyle n}$ cifre (${\displaystyle c_{i}}$) sono le singole cifre, ricordando che ${\displaystyle 8=2^{3}}$ esso si converte in binario nel seguente modo:

1. Si considera il numero ottale ${\displaystyle (c_{1},c_{2},\ldots ,c_{n})_{8}}$, si prendono singolarmente le cifre di cui è composto e si convertono rispettivamente in cifre binarie

Come è ovvio i numeri del sistema in base ottale non possono presentare le cifre 8 e 9; le cifre da 0 a 7 corrispondono esattamente a triplette di zero ed uno del sistema binario.

• Esempio 1: Dato il numero ${\displaystyle 361_{8}}$, il corrispondente numero binario è dato da:

Il numero binario è ${\displaystyle 11110001_{2}}$.

Da binario in ottale

Per convertire un numero dal sistema binario a quello ottale si procede in modo analogo all'esempio precedente:

1. Si considera il numero binario e partendo da destra si divide in gruppi di 3 cifre binarie. Se dopo l'operazione avanzano una o due cifre si aggiungono tanti zeri quanti bastano a coprire un gruppo di tre, per il criterio secondo cui ${\displaystyle 0\ldots 0100=100}$ (v. Sistema numerico binario).
2. Ogni gruppo va poi convertito nel corrispondente numero ottale.

• Esempio 1: Convertire il numero ${\displaystyle 1101001101_{2}}$ in base otto:

Voci correlate

• Conversione tra basi potenze di 2
• Sistemi di numerazione
• Sistema numerico binario
• Sistema numerico decimale
• Sistema numerico esadecimale

Collegamenti esterni

• ottale, su sapere.it, De Agostini.
• (EN) Eric W. Weisstein, Octal, su MathWorld, Wolfram Research.